Über
Trailer zu Bayesian probability theory
Allgemeines zum Kurs
Der Kurs ist interaktiv konzipiert, damit Ihre Lernerfahrung verbessert wird.
Jede Einheit wird durch ein in einer Geschichte eingebettetes Problem motiviert und konzentriert sich auf die Vermittlung der Fähigkeiten und Techniken, um dieses Problem zu lösen.
Seien Sie Teil von Captain Bayes' Crew
, um den Ozean der Ungewissheit und der großen Daten zu befahren, und helfen Sie ihr, die Abenteuer der Wahrscheinlichkeitstheorie zu bestehen.
Lernen Sie die Ideen Ihrer Mitstreiter Bernoulli, Pascal, Laplace und vieler anderer kennen, die Sie auf Ihrer Reise begleiten.
Den Abenteuern von Captain Bayes folgen die Inhaltsvideos, die die Theorien und Konzepte der einzelnen Einheiten vermitteln. Um Sie mit dem neu Gelernten vertraut zu machen, sind interaktive Quizfragen in das Video integriert, die Ihr Wissen praktisch vertiefen.
Lernen Sie außerdem Ernesto
, den Papagei kennen - er wird Sie als Ihr Lernpartner durch den Kurs begleiten und Ihnen Lerntipps und weiterführendes Material geben.
Am Ende jeder Einheit sind Sie bereit, Captain Bayes bei der Lösung der aufgeworfenen Probleme in einem Quiz (5-10 Fragen) zu helfen.
Viel Spaß!
Inhalt
Kursinhalt
Die Hauptmotivation dieses Kurses ist es, ein breiteres Publikum für die Wahrscheinlichkeitstheorie zu begeistern, da sie für alle wissenschaftlichen Bereiche von zentraler Bedeutung ist. Oder wie E.T. Jaynes - einer der bedeutendsten Wahrscheinlichkeitsforscher des letzten Jahrhunderts - es ausdrückte: "Die Wahrscheinlichkeitstheorie ist die Logik der Wissenschaft."
Dieser Kurs macht Sie mit den Methoden der Wahrscheinlichkeitstheorie vertraut und befähigt Sie, mit Unsicherheiten umzugehen, Entscheidungen zu qualifizieren, Wahrscheinlichkeiten zuzuordnen und Parameter und Modelle zu schätzen. Der Bayes'sche Ansatz liefert Techniken zur Aktualisierung der "partiellen Wahrheit".
Insgesamt liefert dieser MOOC die Grundlagen, die für die Bereiche maschinelles Lernen und Data Science notwendig und nützlich sind.
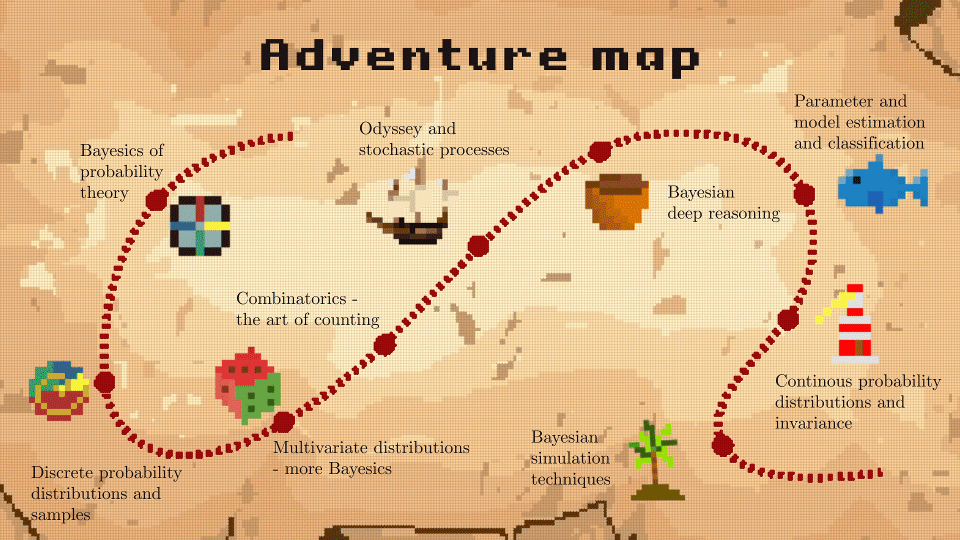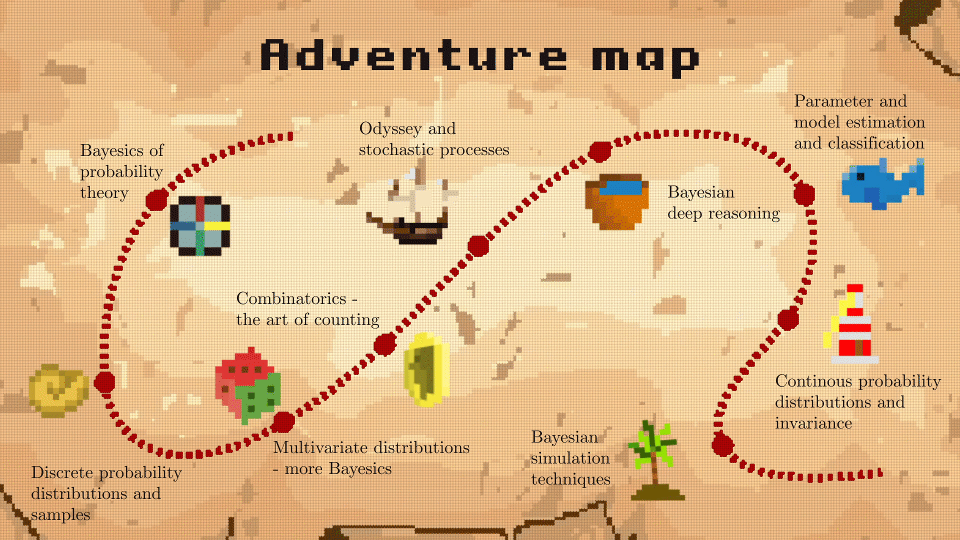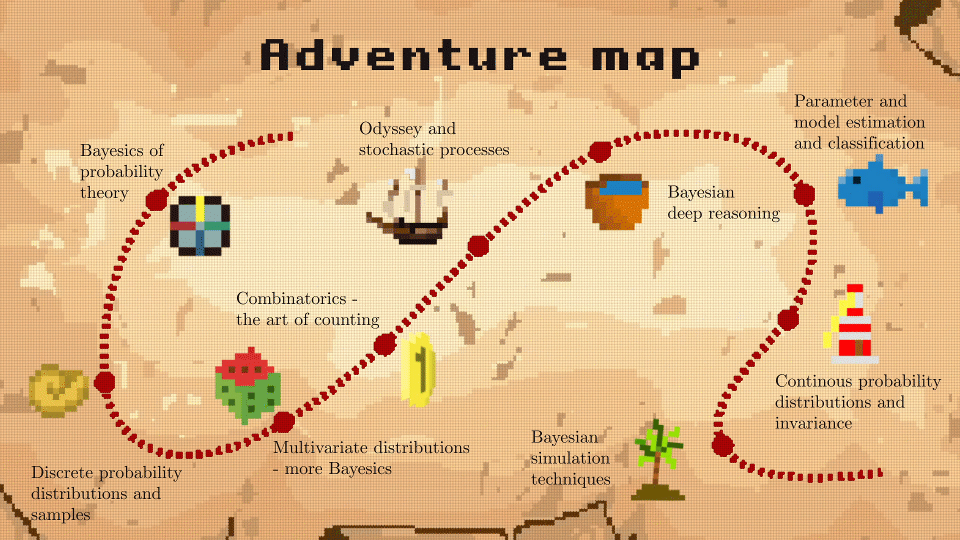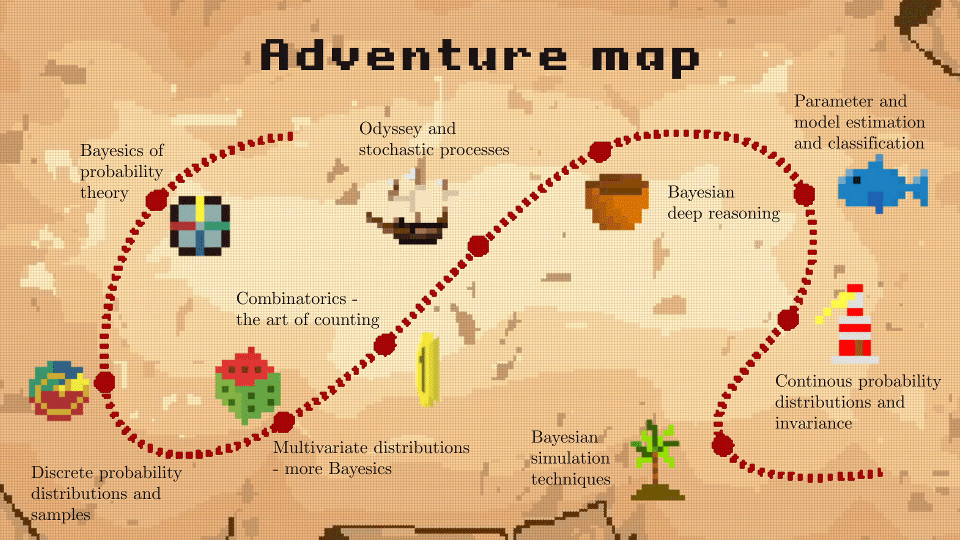
Der Kurs ist in Kapitel unterteilt, die sich mit diskreten und kontinuierlichen Variablen befassen und insgesamt 9 Einheiten umfassen:
- Einheit 1: Bayesics ;-) der Wahrscheinlichkeitstheorie
- Einheit 2: Diskrete Wahrscheinlichkeitsverteilungen und Stichproben
- Einheit 3: Multivariate Verteilungen - noch mehr Bayesics
- Einheit 4: Kombinatorik - Die Kunst des Zählens
- Einheit 5: Odyssee und stochastische Prozesse
- Einheit 6: Bayesianische Argumentationstiefe
- Einheit 7: Parameter- und Modellschätzung und Klassifikation
- Einheit 8: Kontinuierliche Wahrscheinlichkeitsverteilungen und Invarianz
- Einheit 9: Bayessche Simulationstechniken
Lernziele
Das Ziel dieses Kurses ist es, nicht nur die Konzepte der Wahrscheinlichkeitstheorie zu vermitteln, sondern auch kritisches Hinterfragen zu fördern, und Ihnen Kentnisse für eine faktenbasierte Entscheidungsfindung mitzugeben.
Dutzende von Paradoxien zeigen, wie leicht der menschliche Verstand in die Irre geführt werden kann. Daher ist die Fähigkeit, Zahlen und Fakten zu interpretieren, ebenso wichtig wie die Fähigkeit, qualifizierte Schätzungen vorzunehmen. Der Kurs gibt Ihnen das Werkzeug an die Hand, um aus unsicheren und unvollständigen Informationen sensible Schlussfolgerungen zu ziehen.
Der Kurs wird Ihnen insbesondere helfen zu verstehen, wie man Wahrscheinlichkeiten auf klassische und statistische Weise zuordnet, und, was noch wichtiger ist, wie man neue Erkenntnisse nutzt, um Wahrscheinlichkeiten zu aktualisieren und inverse Wahrscheinlichkeitsprobleme zu lösen (Satz von Bayes).
Insbesondere die Aktualisierung des Wissensstandes und die Lösung inverser Probleme sind für das maschinelle Lernen und die Datenanalyse von grundlegender Bedeutung. Weiters werden einige Beispiele im Kurs zeigen, wie man Parameter schätzt und Daten klassifiziert.
Da die korrekte Datenverarbeitung für den Erkenntnisgewinn durch Experimente entscheidend ist, werden auch der Umgang mit Ausreißern und das Ziehen von Schlussfolgerungen aus Stichprobenmengen Themen dieses Kurses sein.
Nach Abschluss des Kurses werden Sie in der Lage sein, probabilistische Aussagen aus (neuen) Daten zu formulieren und mit Hilfe von Simulationen Schlussfolgerungen für stochastische Prozesse zu ziehen.
Aus didaktischer Sicht ist ein wesentliches Ziel, die Diskussion unter den Teilnehmern anzuregen, Ihnen zu helfen, Ihre Ideen und Fragen zu formulieren, und Ihr Engagement zu fördern. Zögern Sie deshalb auch nicht, sich durch unser Forum zu klicken und die eine oder andere Frage zu stellen!
Vorkenntnisse
Die ersten sieben Module behandeln die Grundlagen der Algebra. Die Inhalte sind für Bachelor-Studierende mit mathematischen Grundkenntnissen konzipiert. Für die Einheiten 1 bis 7 sollten die Summenschreibweise, Vektorrechnung und einfache algebraische Umformungen bekannt sein. Die letzten Einheiten über stetige Variablen erfordern grundlegendes Wissen zu Integralen.
Kursablauf
Jede Einheit ist folgendermaßen aufgebaut:
1. Abenteuer von Captain Bayes und ihrer Mannschaft:Ein kurzer Film führt in die Probleme und Themen der Unterrichtseinheit ein.
2. Inhaltliches Video:
Das Inhaltsvideo vermittelt die Sprache, das Wissen und die Theoreme der jeweiligen Einheit, und erklärt die Fragen, die sich Captain Bayes und ihre Mannschaft stellen.
Das Video ist mit kleinen Fragen gespickt, die Ihnen helfen sollen, die besprochenen Konzepte leichter anzuwenden.
3. Interaktive Simulationen:
Zur Vertiefung des Verständnisses werden Ihnen interaktive Simulationen (Pluto-Notebooks mit Julia) zur Verfügung gestellt, die es Ihnen auch ermöglichen, den Code zu übernehmen und selbst zu verändern, wenn Sie daran interessiert sind und damit experimentieren möchten.
4. Forum:
Das Forum ist der Ort, an dem Sie Fragen mit den anderen Teilnehmern diskutieren können.
Wir versuchen, Ihre Diskussionen zu moderieren und Sie nach Möglichkeit mit Antworten auf Ihre Fragen zu unterstützen.
5. Das Quiz:
Das Quiz bildet den Abschluss jeder Einheit und hilft Ihnen, Ihre erworbenen Fähigkeiten unter Beweis zu stellen. Sie werden mit einem Abzeichen belohnt, das als Microcredential fungiert (siehe https://info.badgr.com/) und als Bild heruntergeladen werden kann. Ihre E-Mail-Adresse und die Kursdetails werden in den Metadaten dieses Bildes gespeichert und können mit https://badgecheck.io/ überprüft werden.
Wichtiger Hinweis für Studierende der Lehrveranstaltung "Wahrscheinlichkeitstheorie, Statistik und Datenanalyse" an der Technischen Universität Graz und der Universität Graz:
Um die entsprechenden ECTS dieser Lehrveranstaltung zu erhalten, wird neben der Lehrveranstaltungsprüfung auch die positive Absolvierung dieses MOOCs (75%) dringend empfohlen. Dazu ist es notwendig, dass Sie an der TU Graz bzw. Uni Graz studieren und sich über TUGRAZonline bzw. UNIonline für die entsprechende Lehrveranstaltung anmelden.
Vorlesung an der TU Graz / Uni Graz:
Wahrscheinlichkeitstheorie, Statistik und Datenanalyse - (PHY.E50UF, PHY.E50UB)
Bitte melden Sie sich in jedem Fall mit Ihrer eduID für diesen MOOC an. Dies ist für die Ausstellung eines Zertifikats (Teilnahmebestätigung) unbedingt erforderlich.
Weitere Details entnehmen Sie bitte der Kursbeschreibung bzw. Ihrem Studienplan oder kontaktieren Sie den Vortragenden.
Zertifikat
Für die aktive Teilnahme am Kurs erhalten Sie eine automatische Teilnahmebestätigung (Zertifikat), die Ihren Benutzernamen, den Kurstitel, die Kursdauer sowie die für den Abschluss des Kurses benötigten Stunden enthält. Wir möchten darauf hinweisen, dass dieses Zertifikat lediglich bestätigt, dass der Nutzer mindestens 75 % der Selbsteinschätzungsfragen richtig beantwortet hat.
Darüber hinaus wird ein Badge (Microcredential) für Sie erstellt (siehe https://info.badgr.com/) und kann als Bild heruntergeladen werden. Ihre E-Mail-Adresse und die Kursdaten werden in den Metadaten dieses Bildes gespeichert und können mit https://badgecheck.io/ überprüft werden.
Lizenz
Dieses Werk ist lizenziert unter CC BY 4.0
Kursleitung
Bayes' team
TEAM BAYES:
Wolfgang von der Linden ist ordentlicher Professor und Leiter des Instituts für Theoretische und Computergestützte Physik an der TU Graz. Seine Forschungsschwerpunkte sind stark korrelierte Vielkörperphysik und Bayes'sche Wahrscheinlichkeitstheorie, die in 30 Jahren zu mehr als 100 Arbeiten zu diesem Thema geführt haben. Seine gesammelten Erfahrungen hat er in dem Buch "Bayesian probability theory: applications in the physical sciences." Cambridge University Press, 2014. zusammengefasst.
Projektleiter:
Gerhard Dorn ist Projektmitarbeiter am Institut für Theoretische und Computerbasierte Physik und seit über zehn Jahren in der Lehre tätig. Neben seiner physikalischen Forschung im Bereich des Quantentransports hat er einen starken mathematischen Hintergrund und begeistert sich für das Erzählen von Geschichten in der Wissenschaftskommunikation.
Team Pixel Art:
Gihan El Moazen studiert Biomedical Engineering und hat einen Faible für Pixelkunst und grafisches Design.
Annika Schnell ist eine Physik- und Informatikstudentin, die sich für Spieleentwicklung und Pixelkunst begeistert.
Kreatives Story- und Inhaltsentwicklungsteam:
Tristan Feyer, ein Physikstudent, bringt seine Motivation für die Entwicklung von Geschichten, das Schreiben von Dialogen und das Entwerfen von Landschaften ein.
Gloria Wolkerstorfer beendet ihr Masterstudium der Theoretischen Physik mit dem Schwerpunkt Bayes'sche Wahrscheinlichkeitsrechnung und ist wie Tristan Teil des kreativen Story- und Content-Entwicklungsteams.
Interaktive Simulation und Voice Acting:
Johanna Moser ist eine Physikstudentin, die an der Entwicklung interaktiver Simulationen und den dazugehörigen Geschichten mitwirkt.
Michael Sieberer macht seinen PhD in Physik und hilft bei der Realisierung der Lösung für interaktive Simulationen.
Margit Taibon-Lindheim, Christian Gruber, Florian Payerl und Jakob Hinum-Wagner sind Teil des Sprecherteams und werden von unserem Vocal Coach Reinhard Hütter unterstützt.
Animation und Ton:
Stefan Janisch (LLT TU Graz) ist der Multimedia-Künstler, der an der Postproduktion und Animation der Abenteuerfilme arbeitet.
Martin Haiden (LLT TU Graz) ist der Tontechniker, der für die Tonaufnahme und die Tonproduktion verantwortlich ist.
Melvin Hodzic ist ein Physikstudent, der sich mit der Videobearbeitung und Animation der Unterrichtsvideos beschäftigt.
Gastprofessor - Galleons Figur der Bayes'schen Wahrscheinlichkeitsrechnung
John Skilling, ehemaliger Professor an der University of Cambridge, ist einer der Pioniere der Bayes'schen Wahrscheinlichkeitstheorie und trägt als Erfinder des Nested Sampling zur Einheit über Bayes'sche Simulationstechniken bei - sogar als Teil des Sprecherteams.
Anmelden & Einschreiben Aktuell: 834 Teilnehmer:innen
Kostenlos für alle € 0.00
Partner:innen
Technische Universität Graz
Graz